Marián má vrecko s guľôčkami. Sú v ňom 4 modré, 8 červených a 12 zelených guľôčok. S Jankom hrajú na námestí nasledujúcu hru: Marián za hru zaplatí jedno pivo. Potom vytiahne z vrecka postupne 3 náhodné guľôčky. Prvú guľôčku vráti do vrecka a guľôčky v ňom zamieša a vytiahne druhú. Aj druhú guľôčku vráti naspäť a guľôčky zamieša a vytiahne tretiu. Ak je tretia guľôčka zelená, tak mu Janko vyplatí dve pivá.
Maroško to už nejaký čas sleduje a zdá sa mu, že Marián vyhráva. Má rovnaké vrecko s guľôčkami a tak chce aj on zarobiť. Navrhne, že si to zahrá aj on. Janko súhlasí, ale že budú hrať troška inak. Narozdiel od Mariána, Maroško po vytiahnutí guľôčky nevracia naspäť. (Prvú guľôčku ťahá z 24, druhú z 23, tretiu z 22 guľôčok.) Hra stojí tiež jedno pivo a ak Maroško na tretíkrát vytiahne zelenú guľôčku, tak dostane dve pivá.
Kto má vyššiu šancu na výhru Marián alebo Maroško?
Táto úloha je voľným pokračovaním úloh Spravodlivá hra, Spravodlivá hra 2, Spravodlivá hra 3, Spravodlivá hra 4 – 50 odtieňov rizika, Spravodlivá hra 5 a Spravodlivá hra 5.2, Spravodlivá hra 6 ale aj Sobáš v žalári a Druhá myš si na syre pochutná.
Riešenie
Marián
Pretože Marián vráti prvú aj druhú guľôčku naspäť do vrecka situácia je vždy rovnaká: 12 zelených guľôčok, 24 všetkých guľôčok. Pravdepodobnosť výhry je \(\frac{12}{24}=\frac{1}{2}\). Za dve hry dá Marián dve pivá a v priemere každú druhú hru vyhrá dve pivá, preto pivo nevyhráva ani neprehráva.
Maroško
Maroško to má o čosi náročnejšie. 🙂 Má ale veľa možností, uvediem 4:
- Nepočítať. Hrať iba pre radosť z hry. Veriť v šťastie a svoju výnimočnosť.
- Počítať. V tomto prípade sa to dá zvládnuť. Ak by hádzali 5 krát alebo 10 krát už by to bolo horšie.
- Urobiť si programček, ktorý hru simuluje napríklad 1 000 000 krát a poskytne priemernú pravdepodobnosť. To by pomohlo aj keby mala hra veľa hodov. A programovanie je aj zábava.
- Rozmýšľať. Au.
2
Prvá aj druhá guľôčka môže ľubovoľnej farby, tretia musí byť zelená. To znamená že Maroško má \(3 \times 3\times 1 =9\) výherných možností, ktoré sú zobrazené v tabuľkách. V prvej tabuľke sú jednoduché pravdepodobnosti, napríklad v 1. riadku vidno, že v druhom ťahu je pravdepodobnosť opakovaného vytiahnutia modrej guľôčky nižšia ako v prvom ťahu, pretože v prvom ťahu ubudla modrá guľôčka.
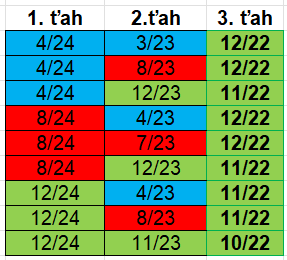
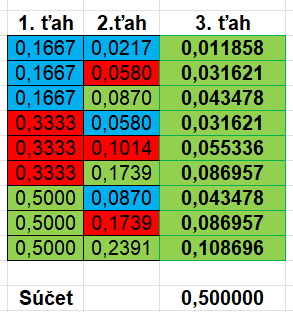
Pravdepodobnosť vytiahnutia modrej guľôčky v 1. aj 2. ťahu je \(\frac{4}{24} \cdot \frac{3}{23}\doteq 0,0217\), čo vidíme v druhej tabuľke (1. riadok, 2. ťah). Obdobne napríklad 3. riadok (modrá-zelená-zelená) je \(\frac{4}{24} \cdot \frac{12}{23}\cdot \frac{11}{22}\doteq 0,0435\).
Súčet pravdepodobností v treťom stĺpci druhej tabuľky je \(\frac{1}{2}\). Takže konečne spravodlivá hra.
Je dobré si všimnúť, že v druhej tabuľke sú niektoré pravdepodobnosti rovnaké. Je jedno či Maroško vytiahne modrú-červenú-zelenú alebo červenú-modrú-zelenú (2. a 4. riadok). V prvej tabuľke vidieť, že ak vymeníme v 2. riadku čitateľ v 1. a 2. ťahu, tak dostaneme 4. riadok. (Ako dobre, že násobenie je komutatívne, t.j. \(3\times4=4\times3\).)
Tabuľka pre všetkých 27 možností vyzerá nasledujúco:
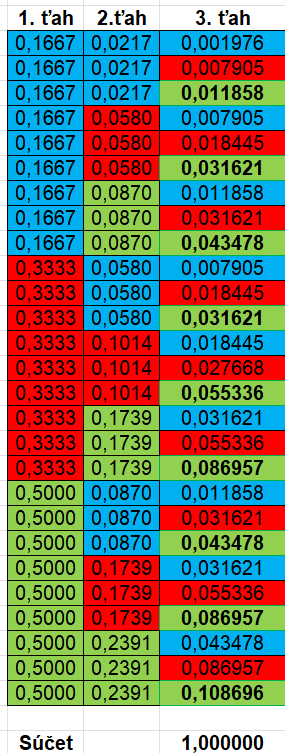
Tu je vidieť, že pravdepodobnosť zelená-modrá-červená je rovnaká ako v prípadoch vyššie. Opäť stačí prehodiť čitatele. Pretože je 6 možností ako vytiahnuť po jednej farbe, tak číslo \(0,031621\) musí byť v tabuľke minimálne 6 krát.
Výpočet sa dá zjednodušiť ak si uvedomíme, že je jedno, či je vytiahnutá modrá alebo červená guľôčka. Môžeme namiesto nich uvažovať 12 ružových. Tabuľka by vyzerala nasledovne:

3
import random
blue = 4
red = 8
green = 12
total_balls = blue + red + green
balls = ['blue'] * blue + ['red'] * red + ['green'] * green
def monte_carlo_simulation(num_simulations):
green_third_count = 0
for _ in range(num_simulations):
drawn_balls = random.sample(balls, 3)
if drawn_balls[2] == 'green':
green_third_count += 1
probability = green_third_count / num_simulations
return probability
# Number of simulations
num_simulations = 100000
probability = monte_carlo_simulation(num_simulations)
print(f'Pravdepodobnosť, že tretia guľôčka bude zelená, je približne {probability:.4f}')
Toto urobil ChatGPT, je to pekné, metodické. Ja by som to urobil inak, určite lepšie a neprehľadnejšie :). (Bez balls a sample. Generoval by som 3 rôzne čísla z [0, total_balls), a ak by posledné bolo menšie ako green, tak +1). Ale stačí.
4
Pravdepodobnosť, že 1. guľôčka bude zelená je \(\frac{1}{2}\). To vieme, lebo Marián ťahá v princípe 1. guľôčku a vidno to aj z prvej tabuľky (posledné tri riadky, 1. stĺpec).
Maroško ťahá farbaA-farbaB-zelená, kde farbaA aj farbaB môžu byť modrá, červená, zelená, môžu byť aj rovnaké. Maroška farbaA ani farbaB nezaujíma, nemusí ich ani vidieť.
V bode 2, v tretej tabuľke sme videli, že Pravdepodobnosť farbaA-farbaB-zelená je taká istá ako pravdepodobnosť zelená-farbaB-farbaA (komutatívny zákon). A pravdepodobnosť, že v 1. ťahu bude zelená je rovnaká ako súčet pravdepodobností zelená-ľubovoľnáFarba-ľubovoľnáFarba = \(\frac{1}{2}\). Preto aj súčet pravdepodobností ľubovoľnáFarba-ľubovoľnáFarba-zelená musí byť \(\frac{1}{2}\).