Táto úloha je voľným pokračovaním úlohy Sedemmíľové čižmy a Sedemmíľové čižmy 2
Janko prekabátil ďalšiu ježibabu – tentokrát to bolo sólo výprava.
V chalúpke našiel 121kg perníka najvyššej kvality (bol to banánový perník). Bolo by ho škoda nechať napospas lesným zvieratkám. Odviezť ho zo stredu lesa by bol problém, našťastie Janko našiel lietajúcu metlu. Táto metla nelieta na čistú mágiu ani benzín ale na lietanie potrebuje perník. Metla má dosť veľkú spotrebu: 1kg na kilometer, bez ohľadu na hmotnosť nákladu. Perník možno prepravovať iba v “palivovej” nádrži, do ktorej sa zmestí maximálne 25kg perníka.
Janko chce na najbližšiu lesnú cestičku, ktorá je vzdialená 15km (vzdušnou čiarou), doviesť čo najviac perníka. Ako to urobí a koľko ho bude?
Riešenie
Základné úvahy.
- Na jeden let to nepôjde. Ak by natankoval 25kg perníka, tak by mal po prílete na cestičku 10kg perníka a už by nemal dosť perníka na cestu späť.
- Koľko natankovať pri spiatočnom lete?
- Koľko natankovať pri lete smerom domov?
- Kde vytvoriť sklad/sklady?
Nasledujúci graf ukazuje kde sa sklady nachádzajú, koľko je v nich perníka a počet letov. Graf je dvojrozmerný, vodorovne je znázornená vzdialenosť skladov (a tam je uvedený počet letov) a zvislo množstvo perníka. Dĺžka úsečiek AB, BC, … nemá význam. Dôležitý je sklon. Čím je strmší, tým je efektivita prepravy horšia (viac spiatočných letov).
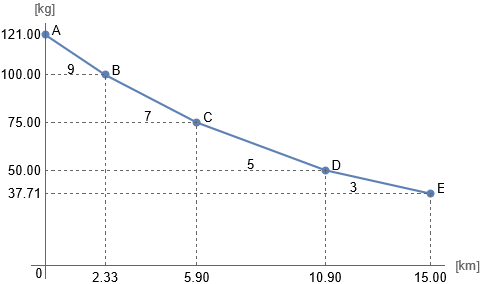
V chalúpke je 21kg perníka navyše oproti optimálnemu množstvu. Preto sklad B bude vo vzdialenosti \(21=9x\), čo je \(\frac{7}{3}=2,\overline{33}\)km.
V sklade B je 100kg perníka, najbližší nižší násobok kapacity nádrže je 75kg. Medzi skladmi B a C je 7 letov. Preto sklad C bude od skladu B vzdialený \(25=7x\), čo je \(\frac{25}{7}\doteq3,57\)km.
Sklad D bude od skladu C vzdialený \(25=5x\), čo je \(\frac{25}{5}=5\)km.
Sklad E by bol vzdialený od skladu D \(25=3x\), čo je \(\frac{25}{3}=8,\overline{33}\)km. To by už bolo za 15km hranicou. Preto od 50kg odčítame trikrát cestu DE: \(50-3 \left(15-\left(\frac{21}{9}+\frac{25}{7}+\frac{25}{5}\right)\right)=\frac{264}{7}\doteq37.7143\)kg
Postup možno zovšeobecniť:
def akoAKolko(kapacita, pernika, vzdialenost):
A = [(0, pernika, vzdialenost)]
while(vzdialenost > 0):
q, m = divmod(pernika, kapacita)
if m == 0:
m = kapacita
q-=1
if m >= (2 * q + 1) * vzdialenost:
A.append((vzdialenost, pernika - vzdialenost * (2 * q + 1),0))
break
else:
pernika -= m
vzdialenost -= m/(2 * q + 1)
A.append((m/(2 * q + 1), pernika, vzdialenost))
return(A)
akoAKolko(25, 121, 15)
#[(0, 121, 15),
# (2.3333333333333335, 100, 12.666666666666666),
# (3.5714285714285716, 75, 9.095238095238095),
# (5.0, 50, 4.095238095238095),
# (4.095238095238095, 37.714285714285715, 0)]