Táto úloha je voľným pokračovaním úlohy Sedemmíľové čižmy.
Janko a Marienka, potom čo prekabátili ďalšiu ježibabu, našli aj v jej perníkovej chalúpke skoro sedemmíľové čižmy. Teda neboli sedemmíľové a vlastne to neboli ani čižmy. Bolo to niečo lepšie. Bola to lietajúca metla. Nie, bolo to niečo oveľa lepšie ako lietajúca metla. Bola to dvojmiestna lietajúca metla. Jedinou nevýhodou je, že nejazdí sama, treba vždy šoféra, ktorý obsadí jedno miesto.
Nájsť najlepší postup, ako sa dve deti dostanú domov na dvojmiestnej lietajúcej metle nie je moc ťažké, pretože na ňu netreba vodičský preukaz a šoférovať ju dokáže aj malé dieťa. Z perníkového väzenia ale oslobodili aj Maťka a potrebujú sa dostať do rodnej dedinky všetci traja.
Aký postup zvoliť ak chcú prísť domov čo najskôr? (Nepočítame čas na odpočinok, prípadne iné zastávky.)
Metla lieta rýchlosťou 25 km/hod a je jedno, či má jedného alebo dvoch pasažierov. Rýchlosť každého dieťaťa pešo je 5 km/hod. Domov je to 100 km.
Okrem toho sú tu ďalšie zaujímavé otázky:
Ako dlho by trvalo, kým dôjdu všetci domov, ak by oslobodili okrem Maťka aj ďalšie dve deti?
Ako dlho by trvalo, kým dôjdu všetci domov, ak by oslobodili okrem Maťka aj ďalšie dve deti a našli by dve dvojmiestne metly?
Ako dlho by trvalo, kým dôjdu všetci domov, ak by ich bolo \(n\) a mali by \(m\) metiel? (\(2\cdot m< n\))
Aká by bola odpoveď na všetky tieto otázky, ak by metla mohla lietať sama?
Riešenie
Z úlohy o 7míľových čižmách vieme, že ak by jedno dieťa šlo pešo viac ako iné, tak by prišlo domov neskoršie. Najlepšie preto bude ak každé prejde pešo rovnakú vzdialenosť a domov prídu všetky naraz.
Táto úloha je samozrejme troška odlišná: Čižmy sme nechávali na mieste, kam si po ne prišlo dieťa. Ak máme lietajúcu metlu, tak sa s ňou šofér môže vrátiť po dieťa, ktoré ostalo vzadu.
Šoféri sa môžu samozrejme striedať, ale metlu bude šoférovať vždy jedno dieťa. To z tejto úvahy vynecháme a úloha „Dvojmiestna metla a 3 deti“ sa zmení na úlohu „Jednomiestna metla (so šoférom) a 2 deti“.
Ak situáciu znázornime podobne ako v predchádzajúcej úlohe, tak dostaneme nasledujúci graf. V tomto prípade šoféruje Maťko, Marienka sa vydá na cestu pešo a Janko je Maťkom odvezený do bodu \(C\) a odtiaľ pokračuje pešo. Z bodu \(C\) ide Maťko s metlou oproti Marienke a vyzdvihne ju v bode \(D\). (Porovnajte s úsečkou \(CD\) v úlohe Sedemmíľové čižmy, tam bola vodorovná, pretože čižmy sa nepohybovali.) Odtiaľ ju dovezie do bodu \(F\) (domov), kde zároveň s nimi príde Janko.
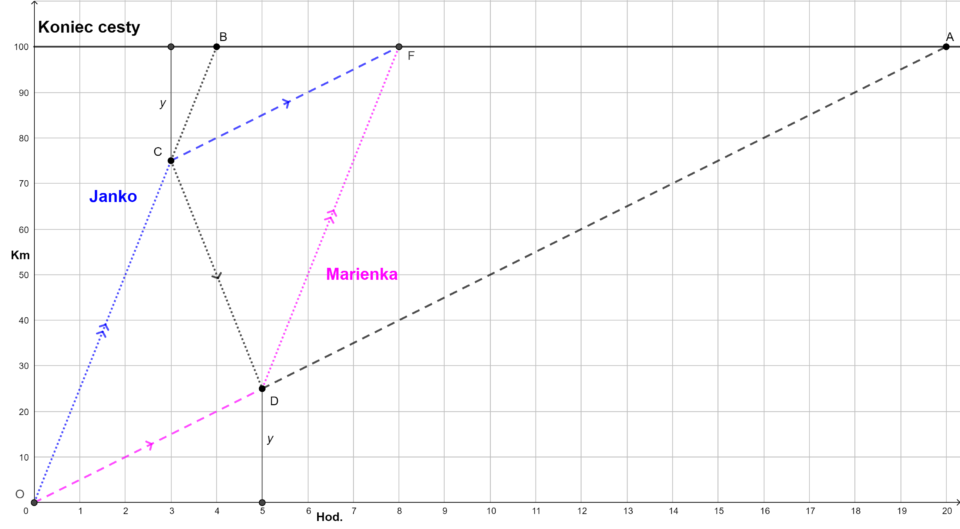
Dôležité je si uvedomiť, že tento graf je dvojrozmerný. Napríklad body \(O\) a \(A\) sú od seba vzdialené na grafe v čase (vodorovná vzdialenosť = 20 hodín) a v priestore (zvislá vzdialenosť = 100 km). Samotná dĺžka úsečky \(OA\) nás nezaujíma, sklon úsečky ale vyjadruje rýchlosť, teda koľko kilometrov pribudne za hodinu (dve, tri, …).
Z grafu vidíme, že ak by niekto letel celú cestu na metle (bodkovaná čiara \(OB\)), prišiel by domov za 4 hodiny. A ak by šiel niekto celú cestu pešo (čiarkovaná čiara \(OA\)), prišiel by domov za 20 hodín. Ak sa im podarí prísť domov naraz, tak im to bude trvať 8 hodín a Janko aj Marienka pôjdu po 5 hodín pešo a po 3 hodiny na metle.
Na to aby sme mohli nakresliť takýto pekný graf, museli sme vypočítať ako ďaleko treba zaviesť Janka, aby sme vyzdvihli Marienku v taký moment, že prídu domov obaja naraz.
Pozrime si trojuholník \(OCD\):
- Bod \(C\) je od perníkovej chalúpky vzdialený \(100-y\) kilometrov.
- Medzi bodmi \(C\) a \(D\) je vzdialenosť, ktorú označíme \(z\), \(z=100-2y\) kilometrov.
- Na základe úvahy, že čas, za ktorý prejde Marienka trasu \(OD\) sa musí rovnať času, za ktorý Maťko na metle preletí trasu \(OC+CD\) môžeme zostrojiť rovnicu (Využijeme známu rovnosť \(t= \frac{s}{v}\), kde \(t\) je čas, \(s\) je dráha a rýchlosť je \(v\)):
\(\frac{y}{5}= \frac{100 – y + (\overbrace{100-2y}^z)}{25}\)
Z čoho dostaneme \(y=25\).
Celková doba prepravy je
\(\frac{y}{5}+\frac{100-y}{25}=8\)
Ak by sme si neuvedomili, že vzdialenosť od konca, kde vysadíme Janka je tá istá ako vzdialenosť od začiatku, kde vyzdvihneme Marienku museli by sme počítať o niečo viac.
Pozrieme sa na to, ako by to vyzeralo pre päť detí. Opäť by jedno robilo šoféra (Maťko) a opäť by každé zo zvyšných štyroch malo prejsť pešo rovnakú vzdialenosť, označme ju \(y\).
Na grafe vidíme, že Maťko odvezie ako prvého Janka (z bodu \(O\) do bodu \(C\)). Janko potom ide pešo až na koniec cesty bod (\(F\)).
Potom čo Maťko vyloží Janka, tak sa vráti po Danku. Danka ide pešo aj s Jankou a Marienkou z bodu \(O\). Maťko ju vyzdvihne v bode (D) a na metle ju odvezie do bodu \(E\). Tam sa Danka pridá k Jankovi, s ktorým pokračuje pešo až na koniec cesty.
Maťko sa potom vráti do bodu \(G\), kde vyzdvihne Janku a odvezie ju do bodu \(H\) – k Jankovi a Danke.
Potom sa vráti po Marienku do bodu \(I\), ktorú odvezie až domov.
Janko prejde pešo vzdialenosť \(y\) na jeden krát, na konci svojho putovania. Marienka ju prejde tiež na jeden krát, na začiatku svojej cesty. Danke a Janke sa táto vzdialenosť rozdelí na dve časti. Danka pôjde pešo trasu \((OD\)+\(EF)\). Janka pôjde pešo trasu \((OG\)+\(HF)\).

Úsečky \(IF\), \(GH\), \(DE\) a \(OC\) sú rovnobežné, pretože po ich dráhe lieta metla rovnakou rýchlosťou (a aj smerom). Z rovnakého dôvodu sú rovnobežné aj úsečky \(CD\), \(EG\), \(HI\). A rovnobežné sú aj úsečky \(CF\) a \(OI\). Preto sú štvoruholníky \(GIFH\), \(GIHE\), \(DGHE\), \(DGEC\) a \(OIFC\) rovnobežníky. Preto musia mať úsečky \(IF\), \(GH\), \(DE\) a \(OC\) rovnakú dĺžku a sklon. A takisto majú rovnakú dĺžku a sklon aj úsečky \(CD\), \(EG\), \(HI\). A tiež \(OD\), \(DG\), \(GI\), \(CE\), \(EH\), \(HF\).
Pamätáte sa ešte? Graf je dvojrozmerný: zvislá vzdialenosť bodov je ich vzdialenosť v priestore (km) a vodorovná vzdialenosť je ich „vzdialenosť“ v čase (hodiny).
Pozrime si trojuholník \(OCD\):
- Body \(D\) a \(G\) rozdeľujú úsečku \(OI\) na tretiny, čo znamená, že bod \(D\) je vzdialený od začiatku cesty \(\frac{y}{3}\) kilometrov.
- Vzdialenosť bodov \(C\) a \(D\) je \(100-y-y/3\).
- Na základe úvahy, že čas, za ktorý prejde Danka trasu \(OD\) sa musí rovnať času, za ktorý Maťko na metle preletí trasu \(OC+CD\) môžeme zostrojiť rovnicu:
\(\frac{y/3}{5}=\frac{(100-y)+(100-y-y/3)}{25}\), z toho dostaneme
\(y=50\)
Celá cesta bude piatim deťom trvať
\(\frac{y}{5}+\frac{100-y}{25}=12\) hodín.
Ak označíme počet detí \(n\) (aj so šoférom, \(n\geq2\)), rýchlosť metly \(v_m\), rýchlosť dieťaťa \(v_p\) a vzdialenosť domov \(s\), tak vo všeobecnosti platí:
\(y=\frac{2 (n-2) s v_p}{(2 n-3) v_p+v_m}\)
Celková doba prepravy je
\(T=\frac{y}{v_p}+\frac{s-y}{v_m}=\frac{(2 n-3) v_m+v_p}{(2 n-3) v_p+v_m} \cdot \frac{s}{v_m}\) hodín.
Ak by sme mali 2 dvojmiestne metly a 5 detí, tak by situácia vyzerala nasledovne:

Plnou čiarou je znázornené cestovanie pešo, čiarkovane Maťkovou metlou a bodkovane Dankinou metlou. Čiarko-bodkovaná čiara znamená, že idú obe metly spolu.
Marienka prejde pešo trasu \(OD\). Maťko odvezie Janka do bodu \(C\) a vráti sa po Marienku, ktorú vyzdvihne v bode \(D\) a odvezie ju až domov (bod \(F\)).
Danka na druhej metle odvezie Janku do bodu \(H\) a vráti sa do bodu \(I\) po Janka, ktorý tam zatiaľ došiel z bodu \(E\).
Výpočet by už nemal robiť problémy:
Pozrime si trojuholník \(OCD\):
- Opäť sú tu rovnobežníky, takže niektoré úsečky sú rovnako dlhé.
- Bod \(D\) je vzdialený od začiatku cesty \(y\) kilometrov.
- Vzdialenosť bodov \(O\) a \(C\) je \((100-y)/2\).
- Vzdialenosť bodov \(C\) a \(D\) je \((100-2y)-(100-y)/2\).
- Na základe úvahy, že čas, za ktorý prejde Marienka trasu \(OD\) sa musí rovnať času, za ktorý Maťko na metle preletí trasu \(OC+CD\) môžeme zostrojiť rovnicu:
\(\frac{y}{5}=\frac{(100-y)/2+(100-2y) – (100-y)/2}{25}\), z toho dostaneme
\(y=\frac{100}{7}\doteq 14,29\) kilometra.
Celá cesta bude piatim deťom trvať
\(\frac{y}{5}+\frac{100-y}{25}=\frac{44}{7}\doteq 6\) hodín a \(17\) minút.
Ak by sme mali 2 dvojmiestne metly a 6 detí, tak by situácia bola veľmi jednoduchá. Ako previesť tri deti jednou metlou bolo vyriešené ako prvé.
Vždy keď je počet detí deliteľný počtom metiel, tak môžeme problém zredukovať. Napríklad, pre 3 metly a 12 detí stačí vyriešiť problém 1 metla a 4 deti.
Problém môžeme zjednodušiť aj keď sú počty metiel a detí súdeliteľné čísla. Napríklad, pre 6 metiel a 15 detí stačí vyriešiť problém 2 metly a 5 deti.
Nasledujúci graf ukazuje situáciu pre 2 metly a 9 detí.

Opäť riešime trojuholník \(OCD\):
\(\frac{y/5}{5}=\frac{(100-y)/2+(100-6y/5) – (100-y)/2}{25}\), z toho dostaneme
\(y=\frac{500}{11}\doteq 45,45\) kilometra.
Celá cesta bude deviatim deťom trvať
\(\frac{y}{5}+\frac{100-y}{25}=\frac{124}{11}\doteq 11\) hodín a \(16\) minút.
Ak označíme počet metiel \(m\), tak
\(y=\frac{2 (n -2m) s v_p}{(2 n-3m) v_p+m v_m}\)
\(T=\frac{y}{v_p}+\frac{s-y}{v_m}=\frac{(2 n-3m) v_m+m v_p}{(2 n-3m) v_p+m v_m} \cdot \frac{s}{v_m}\) hodín.