Táto úloha je zložitejším variantom úlohy Opášme zemeguľu.
Predpokladajme, že Zem je guľa tesne opásaná lanom. Predĺžme lano o jeden centimeter. Potiahneme lano na jednu stranu (ako na obrázku).
Aké veľká bude medzera medzi vrcholom lana a povrchom Zeme?
Aká veľká by bola medzera, ak by sme takto opásali glóbus (obvod 1m, a potom by sme lano predĺžili o 1cm)?
Lano sa nenaťahuje.
Riešenie
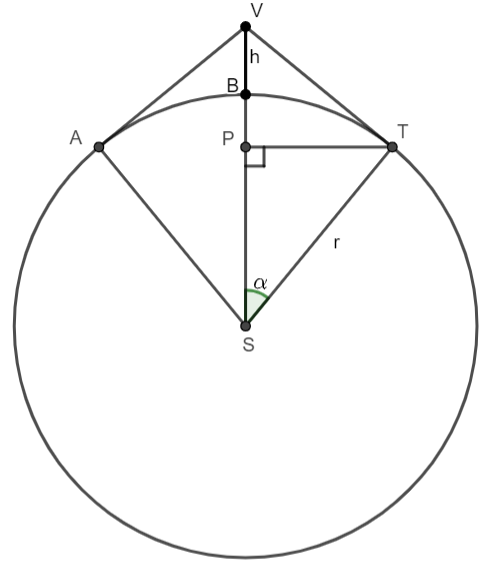
Polomer zemegule v metroch \(r=|ST|=|BS|\). Hľadaná výška medzery je \(h=|BV|\).
Úsečka \(TV\) má dĺžku \(|TV|=|BT|+\frac{1}{200}m\). Je to tak preto, lebo spodný oblúk \(AT\) kopíruje obvod kružnice, preto sa musí \(1cm\) pridať k hornému oblúku \(AT\) a na každú stranu pribudne \(5mm=\frac{5}{1000}m=\frac{1}{200}m\).
Celý obvod kružnice je \(2\pi r\). Chceme zistiť veľkosť oblúka \(|BT|\), ten je daný uhlom \(\alpha\). To je \(\frac{\alpha}{2\pi}\) z celého obvodu:
\(|BT| =2\pi r\cdot \frac{\alpha}{2\pi}= \alpha \cdot r\)
\(|TV|=\alpha \cdot r +\frac{1}{200}\)
\(TV\) musí byť dotyčnica kružnice, ak by nebola, mohli by sme bod \(V\) potiahnuť vyššie. Preto \(ST \perp TV\) a preto je trojuholník \(STV\) pravouhlý.
Môžeme preto využiť funkciu sínus a Pytagorovu vetu:
\(\sin (\alpha)=\frac{|TV|}{|SV|}\)
\(\boxed{\sin (\alpha)=\frac{\alpha\cdot r+\frac{1}{200}}{r+h}}\)
Pytagorova veta tvrdí:
\(|ST|^2 + |TV|^2 = SV^2\)
\(\boxed{r^2+(\alpha \cdot r +\frac{1}{200})^2=(r+h)^2}\)
To nie je ľahké vyriešiť. Ale my sme zostavil dve (orámované) rovnice o dvoch neznámych a na otrockú prácu je vhodný napríklad WolframAlpha. Za pólový polomer \(r\) sme dosadili \(6\ 357km, h \doteq 5,63m\).
Pri glóbuse by to bolo necelých \(h\doteq 1,7cm\).
Výsledok sa dá sa odhadnúť aj bez sínusu. Z bodu \(T\) vedieme kolmicu na \(SV\), priesečník je bod \(P\).
Trojuholníky \(STV\) a \(PTV\) sú podobné, pretože majú jeden spoločný uhol a ďalší uhol je pravý. (Rovnako \(STV\) a \(SPT\).)
Na základe podobnosti trojuholníkov vieme, že
\begin{aligned}
\frac{|PT|}{|TV|}&=\frac{|ST|}{|SV|}\\
|PT|&=\frac{|TV|\cdot|ST|}{|SV|}\\
\text{vieme: }|BT| >|PT| \text{, preto}\\
|BT| >|PT|&=\frac{|TV|\cdot|ST|}{|SV|}\\
|BT|& >\frac{|TV|\cdot|ST|}{|SV|}\\
|BT| \cdot |SV|&>|TV|\cdot|ST|\\
\text{vieme: }|SV|= |ST|+h\\
\text{vieme: }TV|= |BT|+\frac{5}{1000} &\text{, preto}\\
|BT| \cdot (|ST|+h)&>(|BT|+\frac{5}{1000}) |\cdot|ST|\\
|BT| \cdot h&>\frac{5}{1000} \cdot|ST|\\
|BT|&>\frac{5\cdot |ST|}{1000 \cdot h}\\
\frac{5\cdot |ST|}{1000 \cdot h}&<|BT|\\
\boxed{\left(\frac{5\cdot |ST|}{1000 \cdot h}\right)^2}&<|BT|^2
\end{aligned}
Z Pytagorovej vety dostaneme:
\begin{aligned}
{|ST|}^2+|TV|^2&=|SV|^2\\
|TV|^2&=|SV|^2-|ST|^2\\
|TV|^2&=(|ST|+h)^2-|ST|^2\\
|TV|^2&=h\cdot(2\cdot |ST|+h)\\
\text{vieme:}|BT|<|TV|\text{, preto:}\\
|BT|^2<|TV|^2&=h\cdot(2\cdot |ST|+h)\\
|BT|^2&<h\cdot(2\cdot |ST|+h)\\
|BT|^2&<h\cdot(2\cdot |ST|+\mathbf{|ST|})^*\\
|BT|^2&\boxed{<h \cdot3\cdot |ST|}
\end{aligned}
\(^*\)Vieme, že \(h\leq |ST|\), preto môžeme v odhade v druhom riadku odspodu nahradiť posledné \(h\) za \(|ST|\) a znak nerovnosti sa nezmení.
Dáme dokopy orámované nerovnosti a dostaneme:
\begin{aligned}
\left(\frac{5\cdot |ST|}{1000 \cdot h}\right)^2&<|BT|^2<h \cdot3\cdot |ST|\\
\left(\frac{5\cdot |ST|}{1000 \cdot h}\right)^2&<h \cdot3\cdot |ST|\\
\left(\frac{5}{1000}\right)^2\cdot |ST|&<3 \cdot h^3 \\
\frac{25}{10^6}\cdot 6,357 \cdot 10^6 &<3 \cdot h^3 \\
\frac{25\cdot 6,357}{3} &<h^3 \\
3,75m<h
\end{aligned}
Takže aj pri použití \(|BT| >|PT| \) a naozaj hrubom odhade \(h\leq |ST|\) sme zistili, že medzera je celkom veľká.