Rudko má vrece, v ktorom je biely a čierny pešiak a opakuje túto činnosť:
Vytiahne naslepo pešiaka, zaznamená jeho farbu, vráti ho do vreca, dokonale vrece potrasie.
Paľko má rovnaké vrece. A robí to isté.
Môžu dostať napríklad takýto nekonečný rad farieb (Paľko nevidí Rudkov rad a Rudko nevidí Paľkov rad.):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | … | |
| Rudko | b | B | b | b | č | č | č | … |
| Paľko | č | č | Č | b | č | b | b | … |
Paľko povie pozíciu v Rudkovom rade a Rudko povie pozíciu v Paľkovom rade. Ak sú farby rovnaké, tak vyhrajú a stúpne im ELO o 1 bod. Ak sa farby nezhodujú, tak prehrajú a do utorka nesmú hrať šach.
Napríklad:
Ak Rudko povie 3 (Č) a Paľko 2 (B) = prehra – zobrazené v tabuľke.
Ak Rudko povie 1 (č), Paľko 7 (č) = výhra.
Je asi jasné, že náhodné vykrikovanie čísel dá 50% pravdepodobnosť výhry, pretože Rudko určí svojím číslom nejakú farbu a Paľko má 50% šancu sa trafiť.
Je možné zvýšiť pravdepodobnosť výhry, ak sa pred 1. ťahom dohodnú na spoločnej stratégii?
Potom sa už nemôžu dohovárať a ani nepočujú, čo povedal ten druhý.
Pomohlo by im pri výbere stratégie, ak by pravidlá umožňovali, že Paľko počuje číslo, ktoré oznámil Rudko?
Riešenie
Dohoda: Každý povie pozíciu, na ktorej sa mu prvýkrát objavil biely pešiak.
Pravdepodobnosť, že povedia obaja číslo 1 je pravdepodobnosť bieleho pešiaka v prvom ťahu (t.j. \(\frac{1}{2}\)) pre každého:
\(\frac{1}{2}\cdot \frac{1}{2}=\frac{1}{4}\)
Pravdepodobnosť, že povedia obaja číslo 2 je pravdepodobnosť čierneho pešiaka v prvom ťahu a bieleho v druhom ťahu (t.j. \(\frac{1}{4}\)) pre každého:
\(\frac{1}{4}\cdot \frac{1}{4}=\frac{1}{16}\)
Pravdepodobnosť, že povedia obaja číslo 3 je \(\frac{1}{64}\), pravdepodobnosť, že povedia obaja číslo 4 je \(\frac{1}{256}\) atď. Každé ďalšie číslo štvrtinovú pravdepodobnosť oproti predchádzajúcemu.
Takáto postupnosť čísel sa nazýva geometrická. Jej prvý člen a kvocient sú zhodou okolností rovnaké \(a_1=\frac{1}{4}=q\).
Súčet geometrickej postupnosti vypočítame podľa vzorca \(a_1 \cdot \frac{1-q^n}{1-q} \).
Pretože \(-1<q<1\) a \(n\) ide do nekonečna, tak môžeme zjednodušiť \(1-q^n=1\).
\[\sum _{n=1}^{\infty } \frac{1}{4}\cdot\left(\frac{1}{4}\right)^{n-1} =\frac{1}{4}\cdot \frac{1}{1-\frac{1}{4}}=\frac{1}{4}\cdot\frac{4}{3}=\frac{1}{3}\]
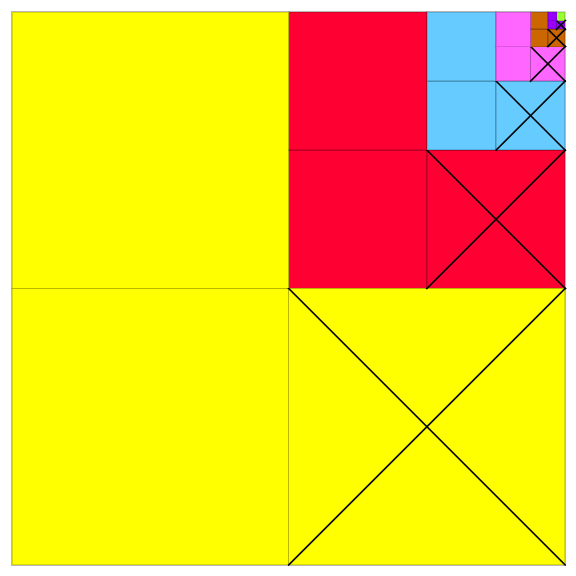
Na obrázku je geometrický dôkaz, že súčet geometrickej postupnosti s kvocientom \(\frac{1}{4}\) je \(\frac{1}{3}\). Prečiarknuté štvorce sú vždy \(\frac{1}{4}\) z nadradeného štvorca a zároveň sú \(\frac{1}{3}\) z trojice viditeľných štvorcov svojej farby. Inak povedané, pôvodný štvorec vieme pokryť trojicami štvorcov o veľkosti \(\frac{1}{4}\) nadradeného štvorca a v celková plocha prečiarknutých štvorcov je \(\frac{1}{3}\) najväčšieho štvorca.
Nech \(z, c, m, r\) sú postupne plochy žltej, červenej, modrej, ružovej oblasti.
\(\frac{1}{3}z +\frac{1}{3} c + \frac{1}{3} m + \frac{1}{3} r+\cdots = \frac{1}{3} (z+ c+ m+r+ \cdots) =\frac{1}{3}\) celého štvorca.
Pravdepodobnosť, že povedia rovnaké číslo je \(\frac{1}{3}\). A ak povedia, tak tieto čísla odkazujú na bielych pešiakov, čo znamená 100% výhru.
Pravdepodobnosť, že nepovedia rovnaké číslo je (1-1/3)=2/3. Nech napríklad Rudko povie menšie číslo, to znamená, že v Paľkovej postupnosti trafil čierneho pešiaka. Paľkove číslo môže ale ukazovať aj na bieleho aj na čierneho pešiaka s pravdepodobnosťou 50%. Preto
\(\frac{1}{3}\cdot 1 + \frac{2}{3}\cdot \frac{1}{2} = \frac{2}{3}= 66,\overline{6}\%\)