Meškanie 6 minút môžeme vyjadriť ako rýchlosť 54 min/hod a 4 minútové nadbiehanie ako rýchlosť 64 min/hod.

Najskôr všeobecná úvaha. Sú dvaja cyklisti, Paľko je 10 km za Rudkom, ktorý je ale pomalší. Paľkova rýchlosť je 30 km/hod a Rudkova 25 km/hod. Koľko bude trvať Paľkovi kým sa dotiahne na Rudka? Zrejme 2 hodiny, každú hodinu stiahne z jeho náskoku 5 km.

A čo keby ich rýchlosti (prvá je vždy Paľkova) boli iba 6 km/hod a 1 km/hod? Alebo 1 000 km/hod. a 995km/hod?

Sú to vždy dve hodiny, nezáleží priamo na rýchlostiach ale na ich rozdiele. Ak pripočítame k ich rýchlostiam to isté kladné alebo záporné číslo, vždy to budú dve hodiny.

Aj 5 km/hod a 0 km/hod (Rudko stojí, pripočítali sme -15). Alebo 3 km/hod a -2 km/hod (Rudko ide naspäť, pripočítali sme -7) a tiež 0 km/hod a -5 km/hod, prípadne -5 km/hod a -10 km/hod. V posledných dvoch prípadoch už ide Rudko rýchlejšie než Paľko.

Kedy najbližšie budú hodinky ukazovať rovnaký čas?

Ako obvykle je niekoľko spôsobov výpočtu.

Prvý spôsob

V ďalšom nám pomôžu špeciálne hodinky, nemajú minútovú ani sekundovú ručičku. Zato majú dve hodinové ručičky. Ručička číslo 1 je z hodiniek Mr. Slim-a a číslo 2 je z hodiniek Mr. Fisher-a.

Ak berieme do úvahy iba vzájomnú vzdialenosť ručičiek po obvode ciferníka a zaujíma nás po akom čase sa stretnú (jedna dobehne druhú), tak je jedno akými rýchlosťami sa pohybujú (rovnako ako pri cyklistoch), dôležitý je len rozdiel rýchlostí. Preto znížime rýchlosť oboch ručičiek o 54min/hod.

Ručička 1 ostane stáť. Ručička 2 má rýchlosť 10 min/hod. a musí prejsť dookola celý ciferník, pretože s ručičkou 1 sú na jednom mieste ale kým sa nepohne, tak sa to neráta. A keď sa pohne, tak už musí ísť iba dopredu.

Celý ciferník je pre hodinovú ručičku túra na 12 hodín. (je to nespravodlivé, pretože pre sekundovú ručičku je to iba 60 sekúnd, pre minútovú ručičku 60 minút, zamysleli ste sa nad tým niekto niekedy?).

 12 hodín je 720 minút a keďže má ručička rýchlosť 10 min/hod, bude jej to trvať 72 hodín, to sú tri dni.

Mohli sme znížiť rýchlosť o 64 min/hod a zastaviť ručičku 2. Ručička 1 by mala rýchlosť -10 min/hod. (šla by opačným smerom). Výpočet by bol až na znamienko rovnaký (pretože sa pohybujeme po kružnici). Ale neurobili sme tak, pretože obvykle sa lepšie ráta s kladnými číslami.

Mierne upravený prvý spôsob

Do špeciálnych hodiniek pridáme tretiu, tentokrát presnú ručičku.

Ručička 1 za presnou zaostáva 6 minút a ručička 2 predbieha tú presnú o 4 minúty. Ručičky 1 a 2 sa preto postupne vzďaľujú od tej presnej a pretože sa od nej vzďaľujú na opačných stranách, tak sa vzďaľujú aj od seba a každú hodinu sa od seba vzdialia o 6 + 4 = 10 minút

Síce sa od seba vzďaľujú ale pretože sa pohybujú po kružnici, tak sa z druhej strany k sebe približujú tou istou rýchlosťou.

Približujú sa k sebe rýchlosťou 10 minút každú hodinu, preto sa musia niekedy stretnúť. Kým sa ale stretnú, musí každá prejsť svoju časť ciferníka a dokopy tieto časti musia dať celý ciferník, teda 12 hodín, to je 720 minút. Priblížiť sa o 10 minút im trvá hodinu. Preto sa stretnú o 72 hodín = tri dni.

Pri tomto výpočte sme pridali presnú ručičku. Nemuseli sme to robiť, stačilo znížiť rýchlosť o 60min/hod aj bez nej. Ale niekedy pomáha krok navyše k lepšej predstave, ako to celé funguje. Presná ručička ostala stáť a ručička 1 sa začala pohybovať zápornou rýchlosťou – teda naspäť a ručička 2 pokračovala pomaly dopredu. Presne ako pri našich cyklistoch 3 km/hod a -2 km/hod aj oni si šli oproti.

Druhý spôsob

Prvý spôsob bol o rozmýšľaní. Druhý spôsob je o obyčajnej matematike.

Obe ručičky začínajú na dvanástke a ručička 2 „šprintuje“ rýchlosťou 64 minút za hodinu dopredu, chystá sa obehnúť celý ciferník a dobehnúť ručičku 1. Ručička 1 sa pohybuje pomalšie, rýchlosťou 54 minút za hodinu. A keďže začínajú na tom istom mieste, tak ručička 2 má handicap 12 hodín = 720 minút (alebo inak povedané ručička 1 má náskok 720 minút), lebo musí obehnúť celý ciferník.

Ak je \(x\) je počet hodín, za ktoré sa stretnú (1 dobehne 2), tak môžeme zostaviť jednoduchú rovnicu:

\(54\cdot x + 720 =64\cdot x\) z toho poľahky aj dostaneme \(x = 72\).

Otázka: Aký čas budú ukazovať?

Za 72 hodín prejde ručička 1

\(54 \cdot 72 = 3888\) minút.

Odrátame celé násobky ciferníka (12 hodín = 720 minút).

\(3888 – 5 \cdot 720 = 288\) minút. Pozri poznámku nižšie.

Ten istý výsledok dostaneme s ručičkou 2.

\(64 \cdot 72=4608\) minút

\(4608 – 6 \cdot 720=288\) minút Pozri poznámku 1 nižšie.

Kde sa na ciferníku nachádza 288 minút?

\(288 = 4 \cdot 60 + 48\) minút

Hodinové ručičky sa stretnú na pozícii kde je hodinová ručička v čase 4 hodiny 48 minút. Teda hodinky budú ukazovať rovnaký čas o 72 hodín ale budú ukazovať 4:48.

Dá sa to vypočítať aj ináč:

\(\frac{288}{720} = 0,4\) hodiny, to je \(0,4 \cdot 60 = 24\) minút.

Hodinové ručičky sa stretnú na pozícii kde je minútová ručička v čase 24 minút.

24 minút na ciferníku pre minútovú ručičku je to isté ako 4 hodiny 48 minút pre hodinovú.

Všimneme si, že to sedí s druhým spôsobom. Ručička 1 je rýchlejšia (-6 min/hod.) než ručička 2 (4 min/hod)

A to nás vedie k tomu, že pozíciu stretu sme mohli vypočítať aj jednoduchšie. Ciferník rozdelíme v pomere 4:6 a pozícia stretu je teda v \(\frac{4}{4+6}\) (je to na pravej polovici, pretože ručička 1 musela prejsť na svojej ceste cez 6).

\(\frac{4}{10}\cdot60 = 24\) minúta, ak chceme minúty.

\(\frac{4}{10}\cdot12 = 4,8\) hodiny, ak chceme hodiny. (\(0,8 \cdot60=48\))

Všetky cesty vedú do Ríma

Poznámka 1:

Časy 1:00, 13:00, 25:00, … ukazujú ručičkové hodiny rovnako. Vždy je to jedna hodina = zvyšok po delení času číslom 12. Je to preto lebo tieto časy možno vyjadriť ako \(12\cdot k+1\).

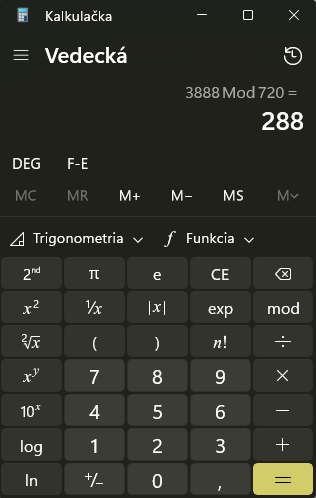
Zvyšok po delení je veľmi dôležitá funkcia, nájdete ju na každej normálnej kalkulačke. Na obrázku je Windows kalkulačka a tlačidlo mod znamená zvyšok po delení. Mod je skratka z modulo.

Kedy najbližšie budú hodinky ukazovať rovnaký a správny čas?

Kedy budú ukazovať správny čas jednotlivé hodinky môžeme zistiť napríklad prvým spôsobom (ale vždy použijeme jednu ručičku presnú a jednu nepresnú) a zafixujeme pomalšiu ručičku (iba preto aby druhá mala kladnú rýchlosť a nám sa ľahšie počítalo).

Zistíme koľko trvá prejsť pohybujúcej sa ručičke ciferník, t. j. 720 minút.

Ak zafixujeme ručičku 1, tak presná ručička má rýchlosť 6 min/hod. Ciferník prejde za 720/6=120 hodín.

Pri zafixovanej presnej ručičke má ručička 2 rýchlosť 4 min/hod. Ciferník prejde za 720/4=180 hodín.

Môžeme to vypočítať samozrejme aj rovnicou, ako v druhom spôsobe prvej otázky.

R1: \(54 \cdot x+720 =60\cdot x\), z toho \(x=120\)

R2: \(64 \cdot x= 60\cdot x+720\), z toho \(x=180\)

Zistili sme nielen to, že hodinky Mr. Slim-a budú ukazovať správny čas o 120 hodín, ale aj že budú ukazovať správny čas každých 120 hodín, teda o 120, 240, 360, 480, 600, 720, … hodín. Podobne hodinky Mr. Fisher-a budú ukazovať správny čas každých 180 hodín, teda o 180, 360, 540, 720, … hodín.

Zvýraznené sú spoločné násobky napríklad: \(720 = 6 \cdot 120 = 4 \cdot 180\). Všimnite si, že čísla 6 a 4 sú poradové čísla v postupnostiach vyššie.

Hľadáme celé kladné čísla \(m\) a \(n\), pre ktoré platí:

\(120 \cdot n=180 \cdot m\)

\(2\cdot n=3 \cdot m\)

Podmienky spĺňa nekonečne veľa dvojíc \(m\) a \(n\). Napríklad, čísla 6 a 4 sú uvedené v príklade o 4 riadky vyššie.

Nás ale zaujíma najmenší spoločný násobok 120 a 180, a to je 360.

Odpoveď: Pomalšie hodinky budú najbližšie ukazovať správny čas o 120 hodín, rýchlejšie o 180 hodín. Naraz ho budú ukazovať o 360 hodín, teda za 15 dní.

Poznámka 2: Všimnite si, že hodinky Mr. Slim-a idú (čo sa ukazovania presného času týka) síce pomalšie ako hodinky Mr. Fisher-a. Ale inak idú rýchlejšie, len opačným smerom -6 min/hod oproti 4 min/hod. Preto prebehnú ciferník skôr.

Otázka: Aký čas budú ukazovať?

Tak to už si hravo “vypočíta” každý sám.