
Nedávno sa v celomraveniskovom turnaji v šachu udeľovala iba prvá cena, tá ale stála za to. Víťaz si mohol zahrať s majstrom sveta 8 partií. Pretože sa jednalo o veľa, tak dvaja finalisti mali hrať viacero partií a víťazom sa mal stať ten, ktorý by ako prvý dosiahol päť výhier (remízy sa nepočítali).
Najskôr ľahká otázka: Koľko (rezultatívnych) partií mohli za týchto podmienok odohrať minimálne a koľko maximálne?
Ťažká otázka: Zápas bol z neznámeho dôvodu predčasne ukončený za stavu 2:4. Je jasné, že nikto nedosiahol 5 výhier, a preto nemohol byť vyhlásený za víťaza. Ale aby cena neprepadla, tak riaditeľ turnaja rozhodol, že cenu rozdelí. Ako? Predpoklad je, že hráči boli a sú rovnako silní a každý má v každej vzájomnej partii šancu vyhrať \(\frac{1}{2}\).
Táto úloha je voľným pokračovaním úloh Mravce – šprintéri, Mravce – maratónci, Mravce a dúha, Mravce a šach a Mravce a šach 2.
Keďže ide o spravodlivé delenie, tak táto úloha súvisí aj s úlohami Úloha o polienkach a Úloha o polienkach 2.
Riešenie
Ľahká otázka: Minimálne 5 (5:0, alebo 0:5), maximálne 9 (5:4 alebo 4:5).
Ťažká otázka je naozaj ťažká. Vyriešiť ju museli až Fermat a Pascal.
Za stavu 2:4 sa mohli odohrať maximálne 3 rezultatívne partie. Označíme mravcov F (Ferko/Fermat, ktorý potrebuje vyhrať 3 partie) a P (Peťko/Pascal, ktorý potrebuje vyhrať 1 partiu).
Je 8 možností ako by mohli tieto 3 partie skončiť:
- FFF – všetky 3 partie vyhrá mravec F.
- FFP – mravec F vyhrá 1. a 2. partiu, mravec P vyhrá poslednú partiu, atď.
- FPF
- FPP
- PFF
- PFP
- PPF
- PPP
Vidíme, že mravec F by celkovo vyhral iba v jedinom prípade – FFF, preto sa výhra delí v pomere 1:7 v prospech mravca P.
Toto bol prístup/vysvetlenie Fermata. Ľudí mätie, že napríklad posledné 4 možnosti považujú za jedinú, P vyhrá v prvej partii a je koniec. To je častá chyba v úsudku, treba brať do úvahy všetky možnosti.
Pascal s Fermatom súhlasil a ponúkol riešenie, ktoré obchádza túto chybu – netreba vysvetľovať prečo nemožno považovať posledné 4 možnosti (alebo 3. a 4. možnosť) za jedinú.
Predpokladajme, že hráči mohli hrať ešte jedno kolo. Toto extra kolo môže viesť k jednej z dvoch možných budúcností, každá s iným rozdelením výhry. Hráči majú rovnaké šance na víťazstvo, preto má každá budúcnosť pravdepodobnosť \(\frac{1}{2}\).
V našom prípade je pravdepodobnosť celkovej výhry mravca F za stavu 2:4:
ak vyhrá F, tak \(\frac{1}{2}\cdot x\), kde x je pravdepodobnosť celkovej výhry mravca F ak je stav 3:4
+
ak vyhrá P, tak \(\frac{1}{2}\cdot 0\) – koniec.
Pravdepodobnosť celkovej výhry mravca F ak je stav 3:4:
ak vyhrá F, tak \(\frac{1}{2}\cdot y\), kde y je pravdepodobnosť celkovej výhry mravca F ak je stav 4:4
+
ak vyhrá P, tak \(\frac{1}{2}\cdot 0\) – koniec.
Je jasné, že y = \(\frac{1}{2}\) (rozhodujúcu partiu vyhrá buď F alebo P).
Preto x = \(\frac{1}{4}\) a celková pravdepodobnosť výhry mravca F za stavu 2:4 je \(\frac{1}{8}\), čo sa zhoduje s Fermatovým rozpisom možností.
Tento postup umožňuje využiť znalosť situácií, kde treba odohrať menší počet partií na určenie riešenia pre hry s väčším počtom. Do jedného riadka by sme to mohli zapísať:
\(\frac{1}{2}\cdot \overbrace{(\frac{1}{2}\cdot\underbrace{(\frac{1}{2}\cdot 1+\frac{1}{2}\cdot 0)}_{3.\ partia,\ stav\ 4:4}+\frac{1}{2}\cdot 0)}^{2.\ partia,\ stav\ 3:4}+\frac{1}{2}\cdot 0\)
Situáciu je možné zobraziť aj v grafe:
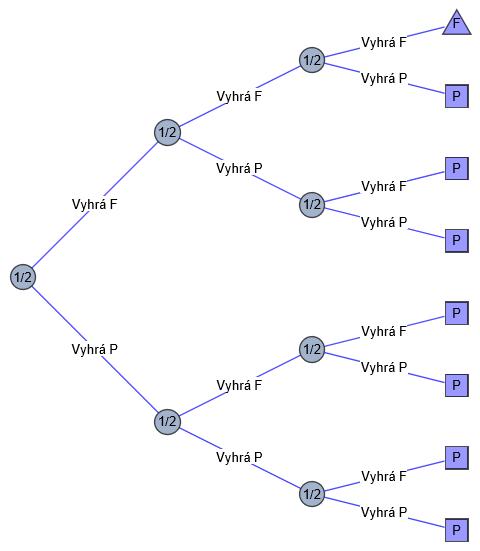
Okrem toho sa Pascal a Fermat správne zhodli na tom, že pomer v akom sa cena rozdelí, nezáleží na počte odohraných partií ale na počte partií, ktoré sa majú ešte odohrať. Teda pri stave 2:4 ak sa hrá do 5 sa výhra rozdelí rovnakým pomerom ako pri stave 11:13 ak sa hrá do 14. Alebo pri stave 1:3 ak sa hrá do 4.