
Ste v člne v strede jazera. Jazero má tvar kruhu. Na brehu je strašidlo. A okrem toho, že je strašné, tak je aj rýchle – je štyrikrát rýchlejšie než vy člne. Ak vás chytí, budete s ním musieť hrať šach (je to strašný amatér, strašne dlho rozmýšľa a podchvíľou vracia ťahy). Na šťastie sa strašidlo bojí vody a tiež viete, že na súši ste o veľa rýchlejší než strašidlo.
Dokážete mu vždy utiecť? Alebo to závisí od veľkosti jazera? Ukážte postup vašej záchrany, prípadne dôkaz, kedy sa to nepodarí.
Riešenie
Uvažujme jazero ako kružnicu s polomerom \(r\), strašidlo je znázornené bodom S.
Priamočiary pokus veslovať zo stredu, smerom od strašidla k bodu E (Exit) nevychádza. V takom prípade by ste prešli vzdialenosť \(r\) a strašidlo by za ten čas prešlo dráhu \(4\cdot r\). Polkružnica má dĺžku \(\pi \cdot r\). Pretože \(4>\pi\), tak to znamená, že v bode E bude strašidlo skôr než vy.
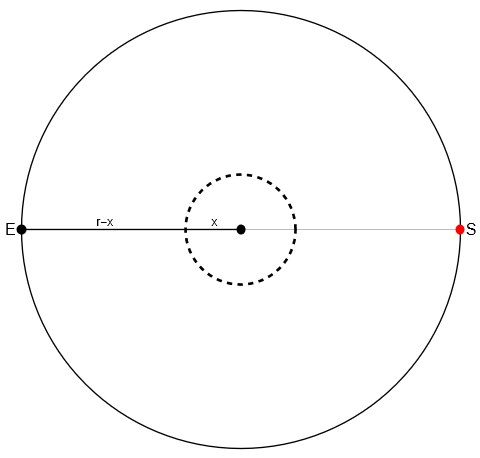
Riešenie: Uvažujme kružnicu, ktorá má oproti obvodu jazera štvrtinový obvod (na obrázku je čiarkovaná). Označme jej polomer \(x\), polomer pôvodnej kružnice je stále \(r\). Porovnajme obvody oboch kružníc.
\(2\cdot\pi\cdot x=\frac{2\cdot\pi\cdot r}{4}\), teda
\(x=\frac{r}{4}\)
Ak ste vo vnútri malej kružnice, tak je vaša obvodová rýchlosť väčšia ako rýchlosť strašidla. Preto sa na vzdialenosť \(x\) od stredu na opačnej strane od strašidla dostanete bez problémov.
Odtiaľ to máte k bodu E už iba \(\frac{3}{4}r\). A pokiaľ vy prejdete túto vzdialenosť, tak strašidlo prejde vzdialenosť
\(4\cdot\frac{3}{4}r = 3\cdot r\). A to je menej ako potrebuje, pretože polkružnica je dlhá \(\pi \cdot r\). (Ako dobre, že \(\pi>3\))
A je jedno, aký je polomer jazera.